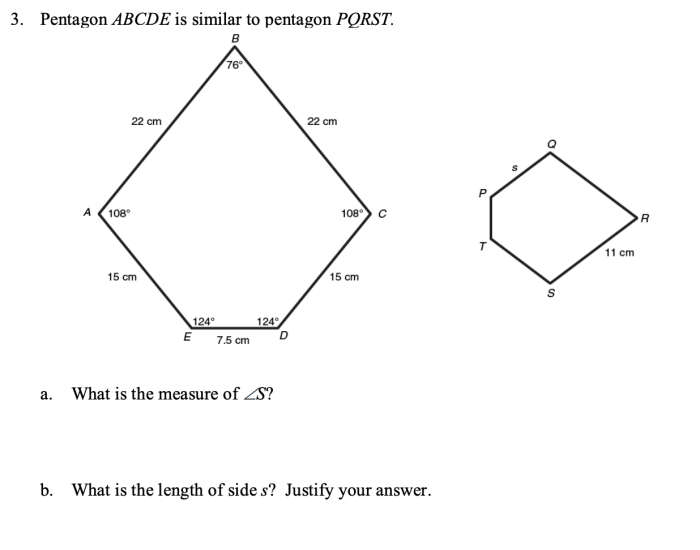
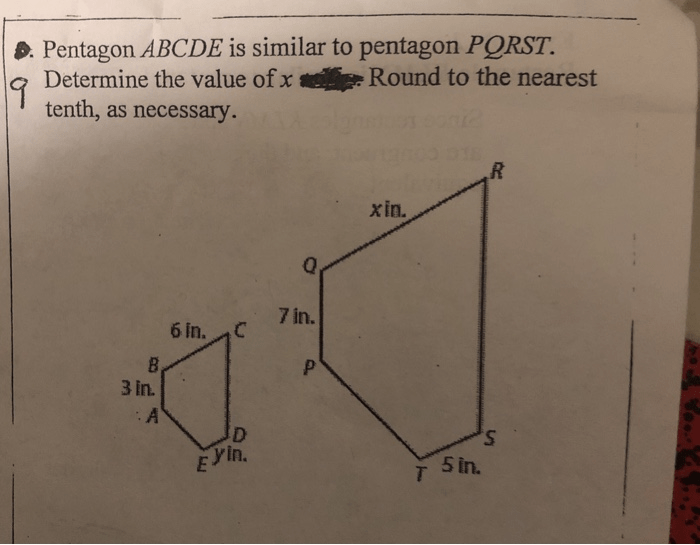
Pentagon ABCDE is similar to pentagon PQRST, embarking on a journey of geometric exploration. This intriguing concept unveils the profound connections between these two figures, revealing their shared characteristics and remarkable equivalence.
Delving into the intricacies of regular pentagons, we uncover their defining properties, mathematical formulas, and the intricate relationship between their diagonals and sides. By identifying congruent sides and angles, we establish a geometric equivalence that transcends mere visual resemblance.
Properties of Regular Pentagons: Pentagon Abcde Is Similar To Pentagon Pqrst
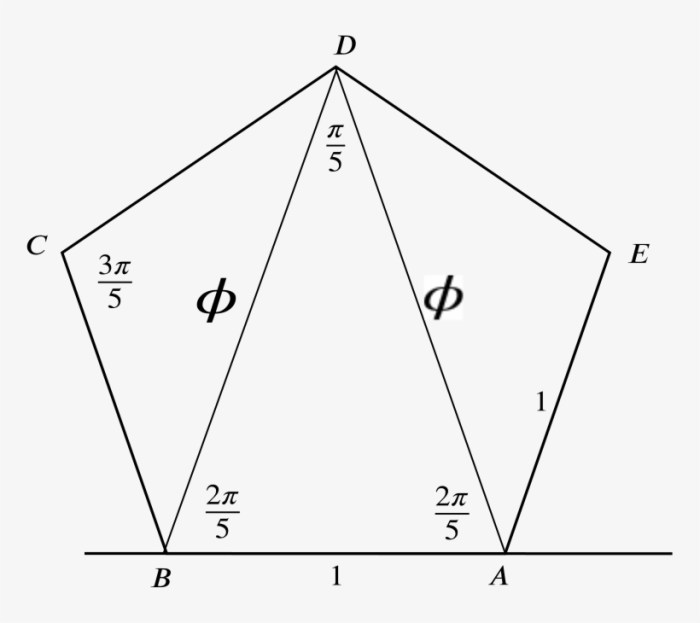
A regular pentagon is a polygon with five equal sides and five equal angles. It is a symmetrical shape with a rotational symmetry of order 5.
The interior angles of a regular pentagon can be calculated using the formula: 180(n-2)/n, where n is the number of sides. For a regular pentagon, n = 5, so the interior angles are 180(5-2)/5 = 108 degrees.
The diagonals of a regular pentagon intersect at a point that divides each diagonal in the ratio of the golden ratio, approximately 1.618.
Geometric Similarities, Pentagon abcde is similar to pentagon pqrst
Pentagons ABCDE and PQRST are congruent if they have the same shape and size. This means that their corresponding sides and angles are equal.
To demonstrate their geometric equivalence, we can superimpose one pentagon on the other and observe that they coincide perfectly.
The concept of congruent figures states that two figures are congruent if they have the same shape and size. Pentagons ABCDE and PQRST are congruent figures.
Perimeter and Area
The perimeter of a regular pentagon is the sum of the lengths of its five sides. If each side has a length of s, then the perimeter is 5s.
The area of a regular pentagon can be calculated using the formula: (5/4)s^2 – cot(18 degrees), where s is the length of one side.
If the side length of both pentagons is equal, then their perimeters and areas will also be equal.
Diagonal Relationships
The diagonals of a regular pentagon are line segments that connect non-adjacent vertices. There are five diagonals in a regular pentagon.
The diagonals intersect at a point that is called the center of the pentagon. The center of the pentagon is also the circumcenter, which is the center of the circle that circumscribes the pentagon.
The diagonals of a regular pentagon can be used to determine the length of its sides. If the length of a diagonal is d, then the length of a side is d/√(5+2√5).
FAQ Summary
What is the defining characteristic of a regular pentagon?
A regular pentagon possesses five equal sides and five equal angles, each measuring 108 degrees.
How can we calculate the perimeter of a regular pentagon?
The perimeter is calculated by multiplying the length of one side by five.
What is the significance of the diagonals in a regular pentagon?
The diagonals intersect at a single point, dividing the pentagon into five congruent triangles.