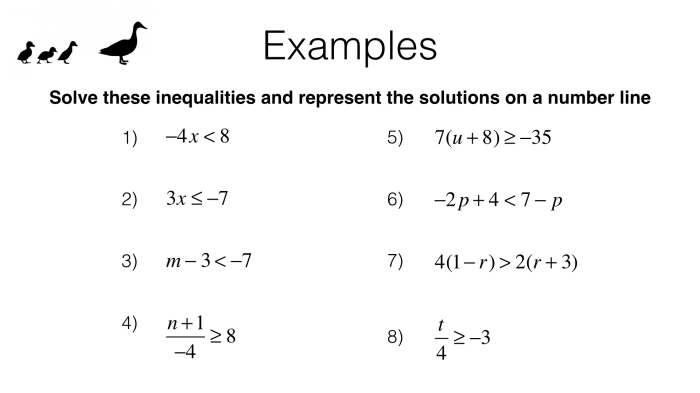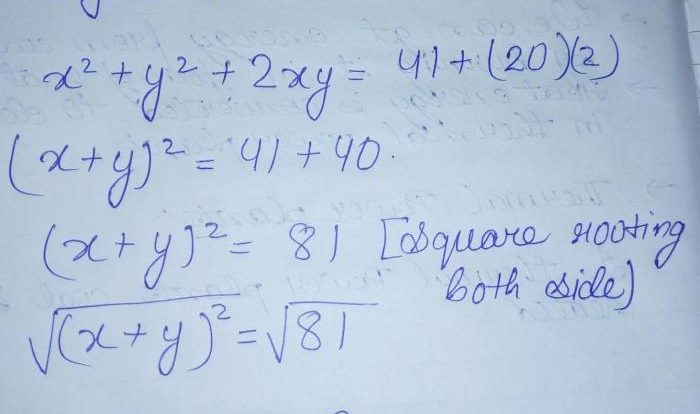Equations and inequalities quick check answer key – Welcome to the world of equations and inequalities! In this comprehensive guide, we will dive deep into the intricacies of these mathematical concepts and provide you with a robust answer key to help you conquer any quick check challenges. From understanding the basics to solving complex equations and inequalities, this guide will equip you with the knowledge and tools you need to excel in this fascinating subject.

As we embark on this mathematical journey, we will explore the fundamental principles of equations and inequalities, unravel their different types, and master the step-by-step process of solving them. Along the way, we will uncover common pitfalls and misconceptions, ensuring that you develop a solid foundation in this essential mathematical domain.

Equations and Inequalities: Equations And Inequalities Quick Check Answer Key

Equations and inequalities are mathematical statements that describe relationships between variables. They are used to solve problems and make predictions.

Equation Basics

An equation is a statement that two expressions are equal to each other. Equations can be written in a variety of forms, but they all have the same basic structure: expression 1 = expression 2.

For example, the equation x + 5 = 10 states that the sum of x and 5 is equal to 10.

There are different types of equations, including:

• Linear equations: Equations that can be written in the form y = mx + b, where m and b are constants.
• Quadratic equations: Equations that can be written in the form y = ax^2 + bx + c, where a, b, and c are constants.
• Polynomial equations: Equations that can be written in the form y = a_nx^n + a_n-1x^n-1 + … + a_1x + a_0, where n is a positive integer and the a_i are constants.

Solving Equations

To solve an equation, we need to find the value of the variable that makes the equation true. We can do this by using a variety of methods, including:

• Substitution: Substituting a value for the variable into the equation and solving for the other variable.
• Elimination: Combining two equations to eliminate one of the variables.
• Factoring: Factoring the equation and solving for the variable.
• Quadratic formula: Using the quadratic formula to solve for the variable in a quadratic equation.

Inequality Basics, Equations and inequalities quick check answer key

An inequality is a statement that two expressions are not equal to each other. Inequalities can be written in a variety of forms, but they all have the same basic structure: expression 1 < expression 2.

For example, the inequality x + 5 < 10 states that the sum of x and 5 is less than 10.

There are different types of inequalities, including:

• Linear inequalities: Inequalities that can be written in the form y < mx + b, where m and b are constants.
• Quadratic inequalities: Inequalities that can be written in the form y < ax^2 + bx + c, where a, b, and c are constants.
• Polynomial inequalities: Inequalities that can be written in the form y < a_nx^n + a_n-1x^n-1 + … + a_1x + a_0, where n is a positive integer and the a_i are constants.

Solving Inequalities

To solve an inequality, we need to find the values of the variable that make the inequality true. We can do this by using a variety of methods, including:

• Substitution: Substituting a value for the variable into the inequality and solving for the other variable.
• Elimination: Combining two inequalities to eliminate one of the variables.
• Factoring: Factoring the inequality and solving for the variable.
• Quadratic formula: Using the quadratic formula to solve for the variable in a quadratic inequality.

Essential Questionnaire

What is the difference between an equation and an inequality?

An equation represents two expressions that are equal to each other, denoted by an equal sign (=). An inequality, on the other hand, represents two expressions that are not equal, denoted by inequality symbols such as less than ( <), greater than (>), less than or equal to (≤), or greater than or equal to (≥).

How do I solve an equation?

Solving an equation involves isolating the variable on one side of the equation while maintaining the equality of both sides. This can be achieved through a series of algebraic operations, such as adding or subtracting the same value from both sides or multiplying or dividing both sides by the same non-zero value.

What are the common errors made when solving inequalities?

Common errors include reversing the inequality symbol when multiplying or dividing by a negative value, not considering all possible cases when solving compound inequalities, and neglecting to check for extraneous solutions.